对Stone-Weierstrass定理的简单讨论
对Stone-Weierstrass定理的简单讨论
Weierstrass逼近
如果 是 上的一个连续实函数,那么便有实多项式 的序列使得 在
上一致地成立,对于连续复函数也可以用复多项式逼近
这是
证明 : 不失一般性地假定
我们再补充定义
取
现在令
注意到这样构造出来的
于是我们就可以试图证明
为了完成这个证明我们现在还需要铺垫
这样就把
这也就是说在这个邻域之外
这样对于足够大的
评注&补充 : 我刚刚看到这一段证明的时候我非常好奇选取这样的
我们首先观察
于是这里我们阐述
那么我们就称之为好核。满足这样条件的”好核”具有单位逼近性(approximation to identity),也就是说
当然这些性质是基于对傅里叶分析的研究而提出的,不过其中的思想对于我们理解本定理的构造是有参考价值的,本题证明中的
Stone对Weierstrass的推广
首先给出一个原始逼近定理的推论,这个推论是接下来推广定理所需要的全部结论(也因此我们其实可以通过其他的路径去证明这个推广的定理)
可以用多项式函数一致逼近
现在我们知道,多项式能够一致地逼近任意连续函数,因此现在希望把多项式地一些能够使逼近成立的性质提取出来,我们希望探究怎么样的一族函数能够使得逼近成立。
我们称定义在集合 上的复函数族 称为代数如果满足以下条件: 对于任意 有 对于任意 有 对于任意 和常数 有
换言之就是满足对加法、乘法、数乘的封闭性。如果族
中存在一列函数 一致收敛到 那么 可以认为是 的一致极限函数(这个词是我自己造的,如有不当请批评)。如果所有一致极限函数都在 中那么称 是一致闭的。 的一切一致极限函数构成的函数族被称为一致闭包。
显然所有多项式构成的集合就是一个代数,因此原始的定理可以被叙述成
仿照点集拓扑中的理论(读者自证不难),容易证明一致闭包是一致闭的。
接下来再追加几个关于函数族的定义
如果对于任意 存在一个函数 使得 ,那么我们称 能分离(区分) 。如果对于任意 存在一个函数 使得 那么我们称 不在 上消失。
这两个关于函数族的条件看起来很弱,实际上通过简单的代数推导我们可以发现二者可以组合出较强的结论。
设 是定义在集合 上的函数的代数, 能分离中的点并且在上不消失,那么对于任意的 和任意的常数 一定存在一个 使得
证明 :
令
最后取
是紧集合 上的实连续函数的代数,如果他能区分点并不消失, 的一致闭包 由 上的全体连续实函数构成。
第一步 如果
对于任意的实数
也就是
我们又知道
第二步 如果
应用第一步的结论这是显然的,只需注意到
这个结论可以被推广到任意有限个函数的最大最小运算。
第三步 对任意的实连续函数
由于
那么根据连续性,一定存在一个包含
根据
于是只需要取
就可以知道这是一个符合条件的构造。
第四步 给定一个实连续函数
对于每一个
同样可以取有限开覆盖
取
于是这样的
因为
讨论&补充 : 这个定理可以推广到复数上,只需要
问题/应用
下面以问题的形式介绍
如果 在 上连续,而且 证明
在 上成立
想法 : 只需注意到
更一般地,如果代数
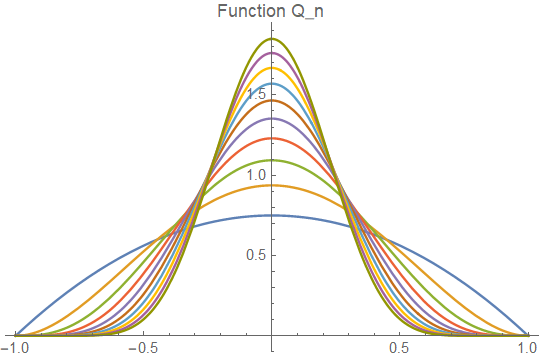
尝试在不证明 逼近的情况下证明 定理。设 定义 证明这个函数列在
一致收敛到
证明 : 注意到关系式
于是 我们可以得到不等关系
这样就可以证明一致收敛性。
周期为 的连续函数可以用三角多项式逼近,即考虑形如 这样一族函数可以一致得逼近任何
周期实函数
想法 : 在紧集
为了做到这一点我们通过映射
讨论 : 假如考虑函数族
这是一个在傅里叶分析中出现的重要定理,这给出了相比 3 中结论更精确的逼近。(下面假定读者了解傅里叶级数相关概念,这些定义可以在数学分析原理第八章中找到)
如果和 是周期为 且黎曼可积的函数并且有 那么可以证明
其中
证明 : 式
于是根据
其他
这个经典的定理还有其他的推广和应用,在以后的文章中可能会涉及。