对Stone-Weierstrass定理的简单讨论

Weierstrass逼近

如果 是 上的一个连续实函数，那么便有实多项式 的序列使得

$$\lim\limits_{n\to \infty} P_n(x) = f(x)$$

在 上一致地成立，对于连续复函数也可以用复多项式逼近

这是 最早发现的逼近定理的形式。

证明 : 不失一般性地假定 并且假设 ，否则令

$$g(x) = f(x) - f(0) - x[f(1)-f(0)]\quad (0\le x\le 1)$$

我们再补充定义 在 以外地区间上取 那么该函数在实轴上一致连续。

取

$$Q_n(x) = \frac{(1-x^2)^n}{\int_{-1}^1 (1 - x^2)^n \,\mathrm{d}x}$$

现在令

$$P_n(x) = \int_{0}^1 f(t) Q_n(t-x) \,\mathrm{d}t$$

注意到这样构造出来的 是关于 多项式。虽然这是一个显然的结论，但是对卷积不熟悉的人可能会产生一定的困惑，所以这里详细展开一下：事实上注意到 是变量，所以把 写成关于 的多项式：

$$\begin{aligned} P_n(x) &= \int_{0}^1 f(t) Q_n(t-x) \,\mathrm{d}t \\ &= \int_{0}^1 f(t) \sum\limits_{k = 0} a_k(t) x^k \,\mathrm{d}t\\ &= \sum\limits_{k = 0} \left[\int_{0}^1 f(t) \sum\limits_{k = 0} a_k(t) \,\mathrm{d}t\right]x^k \end{aligned}$$

于是我们就可以试图证明 逼近 ，为了完成这一点我们需要一些小小的铺垫，对于任取的 由函数的连续性取得 使得 时 。同时假设

为了完成这个证明我们现在还需要铺垫 的性质，也就是估计 的数量级：

$$\begin{aligned} \int_{-1}^1 (1 - x^2)^n \,\mathrm{d}x &= 2\int_0^1(1- x^2)^n\,\mathrm{d}x\\ &\ge 2 \int_0^{\frac{1}{\sqrt n}} (1 - x^2)^n \,\mathrm{d}x\\ &\ge 2 \int_0^{\frac{1}{\sqrt{n}}} (1 - nx^2) \,\mathrm{d}x\\ &=\frac{4}{3\sqrt{n}} \end{aligned}$$

这样就把 数量级控制在了 。对于任意一个 在邻域 之外有

$$Q_n(x) \le\sqrt n(1 - \delta ^ 2) ^n$$

这也就是说在这个邻域之外 一致收敛到 ，这样我们就能开始最后的逼近。

$$\begin{aligned} \left| P_n(x) - f(x) \right| &= \left| \int_{-1}^1 [f(x + t) - f(x)] Q_n(t) \,\mathrm{d}t\right| \\ &\le \int_{-1}^1 |f(x + t) - f(x)|Q_n(t)\,\mathrm{d}t \\ &\le 4M\sqrt{n}(1 - \delta ^ 2) ^ n + \frac{\varepsilon}{2} \end{aligned}$$

这样对于足够大的 上式小于 ，这也就证明了本定理。

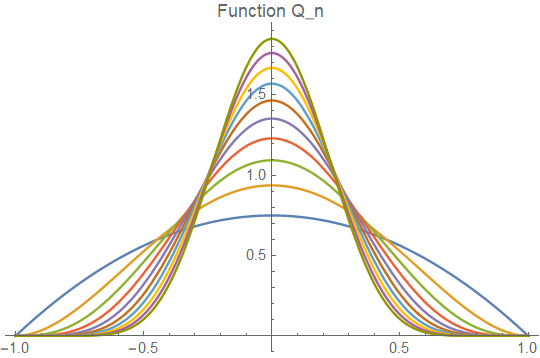
评注&补充 : 我刚刚看到这一段证明的时候我非常好奇选取这样的 的动机是什么呢？我个人认为 在这个部分并没有把这个问题讲清楚。幸好我同时在读 的傅里叶分析导论，其中作者提出的 的概念在很大程度上解答了我的这个疑惑。实际上本定理的证明想法和 证明 级数收敛性时使用的方法如出一辙。

我们首先观察 这个函数，会发现这个函数在 点呈现”峰值”的样貌， 书中用 来形容这种性质。

于是这里我们阐述 的概念：对于任意一组卷积核 如果有

​
关于 是有界的
在任意一个邻域之外积分为零

那么我们就称之为好核。满足这样条件的”好核”具有单位逼近性(approximation to identity)，也就是说

$$\lim\limits_{n\to \infty} (K_n\ast f)(x) = f(x)$$

当然这些性质是基于对傅里叶分析的研究而提出的，不过其中的思想对于我们理解本定理的构造是有参考价值的，本题证明中的 就是构造了这样的一个具有类似好核性质的卷积核。

Stone对Weierstrass的推广

首先给出一个原始逼近定理的推论，这个推论是接下来推广定理所需要的全部结论（也因此我们其实可以通过其他的路径去证明这个推广的定理）

可以用多项式函数一致逼近

现在我们知道，多项式能够一致地逼近任意连续函数，因此现在希望把多项式地一些能够使逼近成立的性质提取出来，我们希望探究怎么样的一族函数能够使得逼近成立。

我们称定义在集合 上的复函数族 称为代数如果满足以下条件：
对于任意 有
对于任意 有
对于任意 和常数 有
换言之就是满足对加法、乘法、数乘的封闭性。

如果族 中存在一列函数 一致收敛到 那么 可以认为是 的一致极限函数（这个词是我自己造的，如有不当请批评）。如果所有一致极限函数都在 中那么称 是一致闭的。 的一切一致极限函数构成的函数族被称为一致闭包。

显然所有多项式构成的集合就是一个代数，因此原始的定理可以被叙述成 上的连续函数集是 上的多项式集的一致闭包，我们接下来要探究的问题就是怎么样的一个代数他的一直闭包是全体连续函数。

仿照点集拓扑中的理论（读者自证不难），容易证明一致闭包是一致闭的。

接下来再追加几个关于函数族的定义

如果对于任意 存在一个函数 使得 ，那么我们称 能分离（区分） 。如果对于任意 存在一个函数 使得 那么我们称 不在 上消失。

这两个关于函数族的条件看起来很弱，实际上通过简单的代数推导我们可以发现二者可以组合出较强的结论。

设 是定义在集合 上的函数的代数， 能分离中的点并且在上不消失，那么对于任意的 和任意的常数 一定存在一个 使得

$$f(x_1)=c_1,\ f(x_2)=c_2$$

证明 : 中一定存在函数 满足

$$g(x_1)\neq g(x_2),\ h(x_1) \neq 0,\ k(x_2) \neq 0$$

令

$$u = [g-g(x_1)]k, v = [g-g(x_2)]h$$

最后取 就可以满足条件

是紧集合 上的实连续函数的代数，如果他能区分点并不消失， 的一致闭包 由 上的全体连续实函数构成。

对这个定理的证明分成了四步

第一步 如果 那么

对于任意的实数 我们知道存在多项式 使得

$$|p(x) - |x|| <\varepsilon$$

也就是 一致地成立

我们又知道 因此我们就证明了

第二步 如果 那么

应用第一步的结论这是显然的，只需注意到

$$\begin{split} \max(f,g) = \frac{f + g}{2}+\frac{|f-g|}{2}\\ \min(f,g) = \frac{f + g}{2}-\frac{|f-g|}{2} \end{split}$$

这个结论可以被推广到任意有限个函数的最大最小运算。

第三步 对任意的实连续函数 以及一点 ，对于任意的 ，便存在着一个函数 满足 并且

$$g_x(t) > t - \varepsilon$$

由于 满足能区分点且不消失，那么 同样满足这个条件，那么对于任意的 我们能够找到 使得

$$h_y(x) = f(x),\quad h_y(y) = f(y)$$

那么根据连续性，一定存在一个包含 的开集 使得

$$h_y(t) > f(t) - \varepsilon\quad(t\in V_y)$$

根据 的紧集性质，这一族开覆盖一定存在有限子覆盖使得

$$K \subset V_{y_1}\cup \cdots\cup V_{y_n}$$

于是只需要取

$$g_x = \max(h_{y_1},\cdots,h_{y_n})$$

就可以知道这是一个符合条件的构造。

第四步 给定一个实连续函数 和 ，那么存在一个函数 使得

$$|h(x) - f(x)| <\varepsilon$$

对于每一个 选取一个满足第三步条件的 由于 的连续性存在开集 使得

$$g_x(t) > f(t) + \varepsilon\quad(t\in V_x)$$

同样可以取有限开覆盖

$$K \subset V_{x_1}\cup \cdots\cup V_{x_n}$$

取

$$h = \min(g_{x_1},\cdots,g_{x_n})$$

于是这样的 就能够满足

$$|h(x) - f(x)| <\varepsilon$$

因为 是一致闭集，所以第四步得到的结论就可以导出定理。

讨论&补充 : 这个定理可以推广到复数上，只需要 满足自伴性质，也就是对共轭运算保持封闭性。

问题/应用

下面以问题的形式介绍 定理的推广和应用

如果 在 上连续，而且

$$\int_0^1 f(x) x^n \,\mathrm{d}x = 0, (n = 0,1,2,\cdots)$$

证明 在 上成立

想法 : 只需注意到

$$\int_0^1 f^2(x) \,\mathrm{d}x = 0$$

更一般地，如果代数 在 上稠密，并且对于任意 都有 ，那么也可以得到 在 上成立。

尝试在不证明 逼近的情况下证明 定理。设 定义

$$P_{n + 1}(x) = P_n(x) + \frac{x^2-P^2_n(x)}{2}$$

证明这个函数列在 一致收敛到

证明 : 注意到关系式

$$\begin{aligned} P_{n + 1} (x) - |x| &= P_n(x) - |x| - \frac{(P_n(x) - |x|)(P_n(x) + |x|)}{2} \\ &=(P_n(x) - |x|)\left(1 - \frac{P_x(x) + |x|}{2}\right)\\ \end{aligned}$$

于是 我们可以得到不等关系 。进一步地，

$$\begin{aligned} P_n (x) - |x| &\le |x|\left(1 - \frac{|x|}{2}\right)^n\\ & \le \frac{2}{n} \left(\frac{n}{n + 1}\right)^{n + 1} \\ & < \frac{2}{n}\\ \end{aligned}$$

这样就可以证明一致收敛性。

周期为 的连续函数可以用三角多项式逼近，即考虑形如

$$\sum\limits_{n = 0}^\infty (A_n \sin nx+B_n \cos nx)$$

这样一族函数可以一致得逼近任何 周期实函数

想法 : 在紧集 上考虑这个问题，显然这是一个代数，并且由于其包含常函数因此这个代数不在 上消失。然而这一代数可以分离几乎任意两个点除了 ，因此这个代数并不是稠密的也就不符合定理得作用条件。考虑到 得周期性我们知道这两个点本质上是等价的，我们需要将 和 等同起来。

为了做到这一点我们通过映射 把 上周期为 的函数当作复平面单位圆 上的函数（也就是考虑 ，其中 是定义在单位圆上的函数）。这样一来三角多项式 是一个自伴代数，并且他在 上分离点、不消失。这就满足复数情形下的 逼近定理。

讨论 : 假如考虑函数族 那么虽然这个函数族能分离点且不消失，但他不是一个自伴代数，因此不能满足条件。

这是一个在傅里叶分析中出现的重要定理，这给出了相比 3 中结论更精确的逼近。（下面假定读者了解傅里叶级数相关概念，这些定义可以在数学分析原理第八章中找到）
如果 和 是周期为 且黎曼可积的函数并且有

$$f(x) \sim \sum_{-\infty}^{\infty} c_n e^{i n x}, \quad g(x) \sim \sum_{-\infty}^{\infty} \gamma_n e^{i n x}$$

那么可以证明

$$\begin{aligned} \lim_{N \rightarrow \infty} \frac{1}{2 \pi} \int_{-\pi}^\pi\left|f(x)-s_N(f ; x)\right|^2 \,\mathrm{d} x&=0\\ \frac{1}{2 \pi} \int_{-\pi}^\pi f(x) \overline{g(x)} \,\mathrm{d} x&=\sum_{-\infty}^{\infty} c_n \bar{\gamma}_n\\ \frac{1}{2 \pi} \int_{-\pi}^\pi|f(x)|^2 \,\mathrm{d} x&=\sum_{-\infty}^{\infty}\left|c_n\right|^2 \end{aligned}$$

其中

证明 : 式由三角版本 逼近定理是显然成立的，式可以在式取 得到。下面证明

$$\begin{aligned} &\quad\frac{1}{2 \pi} \int_{-\pi}^\pi f(x) \overline{g(x)} \,\mathrm{d} x - \sum_{-N}^N c_n \bar{\gamma}_n\\ &= \frac{1}{2 \pi} \int_{-\pi}^\pi f(x) \overline{g(x)} \,\mathrm{d}x - \sum_{-\infty}^\infty c_n e^{inx} \sum_{-N}^N\bar{\gamma}_n e^{-inx}\\ &= \frac{1}{2 \pi} \int_{-\pi}^\pi f(x)\left(\overline{g(x)} - \sum_{-N}^N\bar{\gamma}_n e^{-inx}\right) \,\mathrm{d}x \end{aligned}$$

于是根据 知道上式在 时趋近 ，这就证明了我们想要的结论。

其他

定理也被应用在 判别准则的证明当中，后者被用来处理数列的一致分布问题。

这个经典的定理还有其他的推广和应用，在以后的文章中可能会涉及。